Ball & Beam Control - Digital PID
코딩과 교육/전문코딩 2008. 7. 27. 18:09Ball and Beam problem using PID Control
In this digital control version of the ball and beam experiment, we are going to use the PID control method to design the digital controller. If you refer to the Ball and Beam Modeling page, the open-loop transfer function was derived as
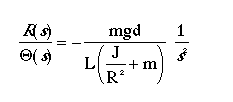
.....g........gravitational acceleration.....9.8 m/s^2
.....d........lever arm offset...............0.03 m
.....L........length of the beam.............1.0 m
.....R........radius of the ball.............0.015 m
.....J........ball's moment of inertia.......9.99e-6 kgm^2
.....R(s).....ball position coordinate (m)
.....theta(s).servo gear angle...............0.25 rad
The design criteria for this problem are:
- Settling time less than 3 seconds
- Overshoot less than 5%
If you refer to any of the PID control problem for continuous systems, the PID transfer function was expressed as
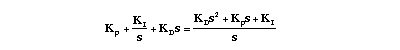
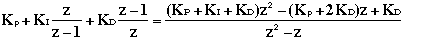
The first thing to do here is to convert the above continuous system transfer function to discrete transfer function. To do this, we are going to use the Matlab function called c2dm. To use this c2dm, we need to specify four arguments: numerator and denominator matrices, sampling time (Ts), and the 'method'. You should already be familiar with how to enter numerator and denominator matrices. The sampling time should be smaller than 1/(30*BW) sec, where BW is the closed-loop bandwidth frequency. The method we will use is the zero-order hold ('zoh'). Assuming that the closed-loop bandwidth frequency is around 1 rad/sec, let the sampling time be 1/50 sec/sample. Now we are ready to use c2dm. Enter the following commands to an m-file.
.....m = 0.111;
.....R = 0.015;
.....g = -9.8;
.....L = 1.0;
.....d = 0.03;
.....J = 9.99e-6;
.....K = (m*g*d)/(L*(J/R^2+m)); %simplifies input
.....num = [-K];
.....den = [1 0 0];
.....Ts = 1/50;
.....[numDz,denDz]= c2dm (num,den,Ts,'zoh')
Running this m-file in the Matlab command window gives you the following matrices.
.....numDz =
..........1.0e-0.4 *
..........0 0.4200 0.4200
.....denDz =
..........1 -2 1
From these matrices, the discrete transfer function can be written as
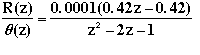
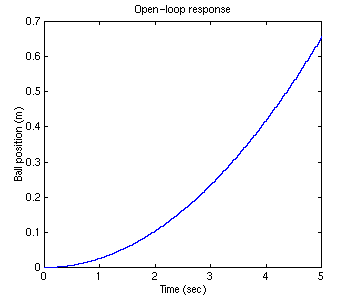
Now we will observe the ball's response to a step input of 0.25 m. To do this, enter the following commands to an new m-file and run it in the command window. You should see the following response.
.....numDz = 0.0001*[0.42 0.42];
.....denDz = [1 -2 1];
.....[x] = dstep(0.25*numDz,denDz,251);
.....t=0:0.02:5;
.....stairs(t,x)
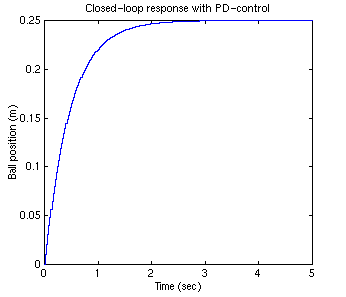
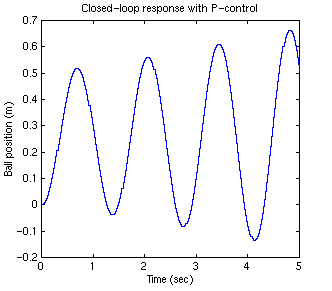
Proportianal Control
Now we will add the proportional control (Kp) to the system and obtain the closed-loop system response. For now let Kp equal to 100 and see what happens to the response. Enter the following commands to an new m-file and run it in the command window.
.....numDz = 0.0001*[0.42 0.42];
.....denDz = [1 -2 1];
.....Kp=100;
.....[numDzC,denDzC]=cloop (Kp*numDz,denDz);
.....[x] = dstep(0.25*numDzC,denDzC,251);
.....t=0:0.02:5;
.....stairs(t,x)
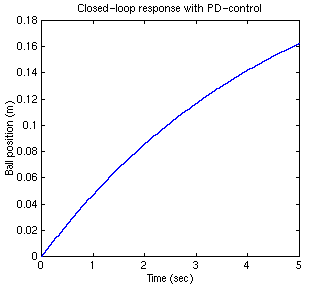
Proportional-Derivative control
Now we will add a derivative term to the controller. Keep the proportional gain (Kp) equal to 100, and let the derivative gain (Kd) equal to 10. Copy the following code to an new m-file and run it to view the system response.
.....numDz = 0.0001*[0.42 0.42];
.....denDz = [1 -2 1];
.....Kp=100;
.....Kd=10;
.....numpd = [Kp+Kd -(Kp+2*Kd) Kd];
.....denpd = [1 1 0];
.....numDnew = conv(numDz,numpd);
.....denDnew = conv(denDz,denpd);
.....[numDnewC,denDnewC] = cloop(numDnew,denDnew);
.....[x] = dstep(0.25*numDnewC,denDnewC,251);
.....t=0:0.02:5;
.....stairs(t,x)