라플라스 변환에 관한 이해
코딩과 교육/전문코딩 2008. 7. 17. 22:17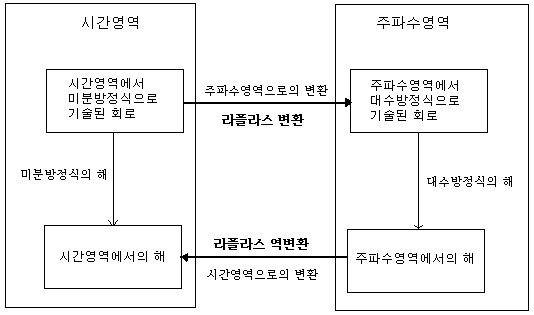
라플라스변환은 시간영역에서 해를 구하기 어려운 미분방정식의 경우 보다 간단한 대수방정식으로 그 해를 구할 수 있게 해주는 특징을 가진다. 즉 복잡한 미분방정식의 해를 직접 구하기보다는 그 방정식을 라플라스 트랜스폼으로 변환시켜 주파수 영역에서 대수방정식으로 만들어 해를 구하고 그것의 역변환을 취해 최종적인 시간영역에서의 해를 구하게 된다.
함수 f(t)의 라플라스 변환은 모든 실수 t ≥ 0 에 대해, 다음과 같은 함수 F(s)로 정의된다.
F(s) = amath L { f } (s) = \int_{0^-}^\infty e^(-s*t) f(t) dt endamath
이때 amath 0^- 는 lim_{epsi->+0} -epsi endamath 의 약자이다. 실제 사용시에는 엄밀히 정확하지는 않은 다음의 표기를 사용하기도 한다.
F(s) = amath L { f(t) } = \int_{0^-}^\infty e^(-s*t) f(t) dt endamath
보통은 Lapalece 변환의 정의를 다음과 같이 사용한다.
...`L[f(t)] = F(s) = \int_0^\infty f(t) e^(-st) dt`
...`s = sigma + j omega`
Laplace 역변환은 다음과 같이 사용한다.
...`L^(-1) F(s) = f(t) = 1 / {j 2 pi } \int_{c-j omega}^\{c+j omega} F(s) e^(st) dt`
시간함수 f(t)에 대한 라플라스변환 함수 F(S) 를 표로 나타낸 것은 다음과 같다.

이울러 f(t) 의 미분, 적분, t 와의 곱 등으로 변형된 형태의 라플라스 변환은 다음과 같다.

참고자료 : 제어시스템과 라플라스변환 공식







